Theoretisches
|
|
Diverses
Theoretisches |
mini-sail
e.V. |
Schwimmfähigkeit und Stabilität von Schiffen
Warum schwimmt ein Schiff?
Ein Beitrag von Willi Pülmanns
Vorbemerkungen:
a.. In den Jahren 2002 /2003 habe ich als Fachlehrer für Schiffstechnik u.a. an der Schule der Wasserschutzpolizei in Hamburg gearbeitet. Im Rahmen dieser Tätigkeit wurde von mir ein Studienbrief gefertigt, dessen Inhalt Gegenstand dieses Artikels ist. In einigen Bereichen wurde die Thematik vereinfacht, in anderen ausführlicher beschrieben, jeweils in Abhängigkeit davon, was für einen Beamten der Wasserschutzpolizei von Bedeutung sein mag. Der Schwerpunkt meiner Betrachtungen liegt demnach naturgemäß im Bereich der Binnenschiffe. Letztendlich ist es aber gleichgültig, um welche Art Schiff es sich handelt, da alles gesagte auf alle Schiffe, auch auf die ganz kleinen (nämlich unsere) anwendbar ist.
b.. Im Kapitel 2, Stabilität wird zwischen Form- und Gewichtsstabilität unterschieden. Für uns als Modellbauer ist die Gewichtsstabilität regelmäßig zutreffend. Per definitionem ist ein Schiff entweder nur das eine, oder nur das andere. Zumindest 1 mir bekannter (und von mir hochgeschätzter) Mini-Sailor hat jetzt aber bestimmt schon ein „...ja aber...!“ auf den Lippen. Ich stimme ihm zu, wenn er sagt, daß ein vom Prinzip her gewichtsstabiles Schiff an Stabilität gewinnt, wenn man z.B. dessen Rumpf verbreitert. Dies ist ein Merkmal, das eigentlich auf ein formstabiles Schiff deutet, da diese Schiffe den größten Teil ihrer Stabilität aus ihrer großen Breite im Verhältnis zum Tiefgang beziehen. Dennoch liegt hier keine „Mischform“ der Stabilitätsarten vor, und wer die Definitionen der beiden Begriffe gelesen hat, der wird feststellen, daß es sich bei einem gewichtsstabilen Schiff mit verbreiterten Rumpf immer noch um ein gewichtsstabiles Schiff handelt, da die Stabilitätsform sich ausschließlich über die Lage der beiden Schwerpunkte im Schiff definiert.

| 1 Schwimmfähigkeit |
| 1.1 Die physikalischen Grundlagen der Schwimmfähigkeit |
| Warum schwimmt ein Körper? |
Archimedes (287- 212 v.Chr.) stellte fest:
Merke:
| Ein Körper, der (vollständig) in Flüssigkeit getaucht wird,
verdrängt genau soviel Flüssigkeitsvolumen, wie er selbst an Volumen einnimmt. |
Ein Würfel, mit einer Kantenlänge von genau 10cm verdrängt demnach genau 1 Liter Wasser (10cm
x 10cm x 10cm = 1000cm³ oder 1 dm³ oder 1 Liter) vorausgesetzt, er wird vollständig
untergetaucht. Nun läßt sich untersuchen, ob 1 Liter Körper schwerer oder leichter ist, als 1
Liter Wasser. Dies kann man bei jedem Material und unabhängig von der Beschaffenheit des Körpers
tun.
Tatsächlich legte man ein bestimmtes Volumen fest und wog dieses Volumen des zu untersuchenden
Materials ab. Das ermittelte Gewicht ist das sog. Spezifische Gewicht und endlich eine Größe, mit
der wir unser oben angesprochenes Verhältnis genau genug beschreiben können, nämlich als Quotient
aus Masse und Volumen:
| Spezifisches Gewicht = Masse (kg) : Volumen (dm³) |
(für die Bezeichnung des Spezifischen Gewichts sind auch andere Masse- und Volumeneinheiten zulässig, z.B. kg/m³, oder g/cm³; anstelle Spezifisches Gewicht wird auch der Ausdruck Dichte verwendet) Kommen wir auf unsere anfangs gemachte Aussage zurück (die übrigens nicht ganz falsch war, aber eben nur die halbe Wahrheit). Wenn wir die Aussage nur wenig abändern, wird sie präzise:
Merke:
| Ein Körper schwimmt,
wenn sein spezifisches Gewicht (oder seine Dichte) geringer ist, als das (die) des Wassers. |
Ja, und wieso schwimmt dann ein modernes Schiff? Das ist doch überwiegend aus Eisen gebaut und
das hat ein spezifisches Gewicht von ca. 7 kg/dm³. Eine kleine Schraube, die ich ohne Weiteres
tragen kann, geht unter und ein Schiff, daß ich ohne Technik nicht auch nur im Geringsten bewegen
kann schwimmt!
Nun, schauen wir uns den Aufbau eines Schiffes einmal genauer an. Wir stellen fest, daß ein
solches Schiff in der Gesamtheit betrachtet nicht nur aus Eisen, sondern auch aus den
verschiedensten anderen Materialien besteht, in der Hauptsache jedoch aus umbauter Luft. Wir
werden uns wohl ohne weiteres darauf verständigen können, daß Luft ein sehr niedriges
spezifisches Gewicht hat.
Bei einem Schiff ist also mit einer relativ geringen Masse an Material ein sehr großes Volumen
umbaut worden. Wir erinnern uns an den zuvor erarbeiteten Grundsatz:
| Spezifisches Gewicht = Masse (kg) : Volumen (dm³) |
Bei einem Binnenschiff durchschnittlicher Größe können wir dessen Masse durchaus mit 200 Tonnen, d.h. 200 000 kg annehmen. Umbaut ist aber mit dieser Masse ein Volumen von, nehmen wir an 2000 m³ oder 2 000 000 dm³. Setzen wir die Werte doch einmal in unseren Grundsatz ein:
| Spezifisches Gewicht = 200 000 kg : 2 000 000 dm³
Spezifisches Gewicht = 0,1 kg/dm³ |
Siehe da, das Spezifische Gewicht des Schiffes in unserem Beispiel ist also weit geringer als 1 kg/dm³ und damit auch geringer, als das des Wassers. Es schwimmt. Dabei haben wir nicht etwa durch einen Rechentrick das Spezifische Gewicht von Eisen so zurecht frisiert, daß es schwimmt, sondern wir haben prinzipiell nichts anderes gemacht, als das durchschnittliche Spezifische Gewicht des Schiffes, mit all seinen unterschiedlich schweren Massen bestimmt.
Fassen wir kurz zusammen:Die bisherigen Erkenntnisse sind aber im allerstrengsten und wissenschaftlichen Sinne
lediglich Beobachtungen. Sie sind absolut richtig, können für sich genommen jedoch immer noch
nicht ausreichend erklären, warum ein Körper schwimmt. Ein wichtiger Aspekt blieb nämlich bisher
unberücksichtigt.
Vielleicht haben Sie auch schon einmal den Ausdruck gehört: „...das Wasser trägt!“
Was sich hinter dieser schlichten Aussage verbirgt, wird eigentlich erst klar, wenn der Mensch
die Aufgabe übernehmen soll, die sonst dem Wasser zukommt, nämlich das Tragen. Um z.B. ein Schiff
aus dem Wasser zu heben muß man einen Kran haben, der vor allen anderen Attributen eines haben
muß: Kraft!!! Seine Kraft muß so groß sein, daß sie mindestens die Gewichtskraft des angehängten
Schiffes nicht nur im Wortsinne aufhebt.
Bei unserem Kran kommt die Kraft aus der Antriebsmaschine. Woher kommt sie beim Wasser? Auch hier
gilt, daß der Gewichtskraft des Schiffes mindestens eine gleich große Kraft entgegenstehen muß.
Eine solche Kraft ist tatsächlich existent. Sie nennt sich Auftriebskraft.
Auch hierzu gibt es eine auf Archimedes zurückgehende Erkenntniss:
Merke:
| Auf einen Körper, der in Flüssigkeit* getaucht wird, wirkt eine
Auftriebskraft.
Diese entspricht der Gewichtskraft der vom Körper verdrängten Flüssigkeit. |
*Streng genommen müßte hier stehen: „...der in Flüssigkeit oder in ein Gas getaucht wird...“. Tatsächlich entsteht auch in der Luft ein Auftrieb, der jedoch so klein ist, daß er in den Bereichen, mit denen wir uns hier beschäftigen vernachlässigt werden kann.
Merke:Ein steigender Körper durchbricht irgendwann die Wasseroberfläche. Von diesem Moment an verringert sich das Volumen des eingetauchten Körpers. Der Körper steigt solange, bis das noch eingetauchte Volumen eine Flüssigkeitsmenge verdrängt, deren Gewicht seinem eigenen entspricht. Auftrieb (also die Gewichtskraft der verdrängten Flüssigkeitsmenge) und Gewicht des Körpers heben sich dann exakt auf und ein Teil des Körpervolumens ist oberhalb der Wasserlinie; er schwimmt!
Merke:
| Ein schwimmender Körper wiegt genau so viel, wie das von ihm verdrängte Wasser. |
| Woher kommt die Auftriebskraft? |
Wenn Sie schon einmal im Schwimmbad getaucht sind, so macht sich ab einer gewissen Tiefe auf
ihren Ohren ein unangenehmes Gefühl bemerkbar. Wir sagen dann, daß der Wasserdruck uns
Ohrenschmerzen bereitet. Das rührt daher, daß sich über uns eine Menge Wasser befindet, das mit
seinem Gewicht auf uns lastet, also vom Schweredruck des Wassers.
Weiter stellen wir fest, daß der Druck auf unseren Ohren um so größer wird, je tiefer wir
tauchen. Es befindet sich eine immer größere Wassermenge über uns.
Der Schweredruck des Wassers wirkt aber nicht nur von oben auf uns, sondern aus allen
Richtungen.
Stellen wir uns einen Würfel vor, mit einer Kantenlänge von 10 cm. Diesen tauchen wir wieder
in ein mit Wasser gefülltes Gefäß. Jetzt wirkt der Schweredruck des Wassers von allen Seiten auf
den Würfel. Den Drücken, die seitlich auf den Würfel wirken, steht ein exakt gleich großer Druck
genau gegenüber. Diese Drücke heben sich auf und sind für unsere Untersuchung der Auftriebskraft
nicht weiter von Bedeutung. Ganz anders sieht es mit dem Druck, der von oben und unten auf den
Würfel wirkt aus.
Auf die obere Fläche des Würfels lastet eine bestimmte Wassermenge und damit ein bestimmter
Druck. Auf die untere Fläche wirkt auch ein Druck. Da sich die untere Fläche des Würfels jedoch
in tieferem Wasser befindet, als die obere, ist auch der Druck, der auf sie wirkt ein
größerer.
| F | |
| p = | – |
| A |
Da die Flächen (A) unseres Würfels alle gleich groß sind, der Druck sich aber mit der Wassertiefe trotzdem verändert hat, kann diese Veränderung nur erklärt werden, wenn sich die wirkende Kraft (F) verändert hat. Das ist auch so, auf die tiefer gelegene Fläche unseres Würfels wirkt eine größere Kraft, als auf die obere. Die Differenz zwischen den beiden Kräften ist unsere Auftriebskraft. Übrigens: diese Differenz ist in allen Tiefen gleich groß, egal ob Sie sie im Mariannengraben, oder bei sich zu Hause in der Badewanne messen würden.
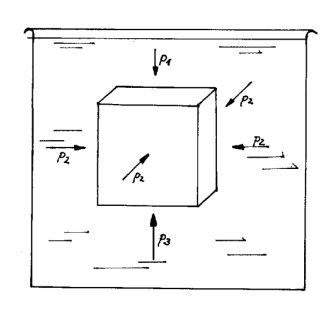 |
Skizze:
Würfel im Wasser mit wirkenden Kräften p = Wasserdruck in der Skizze gilt: - alle p2 sind gleich groß und heben sich auf - p1 < p3 |
Wir sind fast durch mit den physikalischen Grundlagen für die Schwimmfähigkeit. Hier an dieser Stelle sei nur noch kurz darauf hingewiesen, daß wir immer dann, wenn wir von Kräften reden, uns auch darüber im Klaren sein müssen, in welche Richtung diese wirken und wo sie angreifen.
Die Gewichtskraft eines Körpers kann man sich als in einem Punkt angreifend vorstellen. Dieser Punkt ist der Gewichtsschwerpunkt des Körpers. Die Gewichtskraft wirkt senkrecht nach unten, in Richtung Erdmittelpunkt (mittlerweile gibt es Annahmen, daß das nicht immer so ist, sondern daß es auf der Erde Gravitationszentren gibt, die nicht im Kern liegen, so daß die Gewichtskraft nicht in jedem Fall genau nach unten wirkt. Für unsere Betrachtungen vernachlässigen wir diesen Aspekt aber einfach mal).
Die Auftriebskraft greift ebenfalls in einem Punkt an. Auch dieser Punkt ist Schwerpunkt. Hierbei handelt es sich jedoch um einen anderen Schwerpunkt. Wir betrachten nämlich nicht mehr den gesamten Körper, sondern nur noch den Teil des Körpers, der in das Wasser eingetaucht ist. Da das eingetauchte Volumen eines Schiffes genau den Platz einnimmt, den vorher das Wasser eingenommen hatte, kann man sich vorstellen, daß das verdrängte Wasser auch die gleiche Form wie das eingetauchte Schiffsvolumen hat. Diese imaginäre Form aus Wasser hätte ihrerseits natürlich auch einen Schwerpunkt. Durch äußere Einflussfaktoren kann die Lage des Körpers im Wasser verändert werden. Damit ändert sich auch die Form des eingetauchten Volumens und mit ihm, die Lage des Schwerpunktes. Der Schwerpunkt von dem hier die Rede ist, wird daher auch Formschwerpunkt genannt.
Die Auftriebskraft wirkt der Gewichtskraft genau entgegen, also senkrecht nach oben.
Wenn Sie alles verstanden haben, dann sollten Sie in der Lage sein, die folgenden kleinen Kontrollfragen zu beantworten:
| 1.2 die Bedeutung der physikalischen Grundlagen für den Schiffsbetrieb |
Im vorherigen Abschnitt haben wir festgestellt, daß ein Körper schwimmt, wenn sein
spezifisches Gewicht geringer ist, als das des Wassers. Da ein Schiff aus vielen Baustoffen
besteht und zudem noch ein großer Hohlraum ist, haben wir sein spezifisches Gewicht als den
Quotient aus Masse (kg) und Volumen beschrieben und somit sein durchschnittliches spezifisches
Gewicht bestimmt.
Dieses durchschnittliche spezifische Gewicht ist keineswegs immer gleich, sondern kann verändert
werden. In der Regel geschieht das durch Zuladung irgendwelcher Güter.
Schauen wir uns noch einmal das Zahlenbeispiel eines leeren Binnenschiffes an:
| Leergewicht: 200 t = 200 000 kg
Volumen: 2 000 000 dm³ |
Daraus folgt ein durchschnittliches spezifisches Gewicht von 0,1 kg/dm³ (Spezifisches Gewicht
= Masse : Volumen).
Jetzt soll mit diesem Binnenschiff eine Ladung Sojaschrot mit einem Gewicht, genauer gesagt einer
Masse von 1000 t transportiert werden. Damit erreicht unser Binnenschiff eine Gesamtmasse von
1200 t, oder 1 200 000 kg. Das hat Folgen für unser spezifisches Gewicht:
| spezifisches Gewicht = 1 200 000 kg : 2 000 000 dm³
spezifisches Gewicht = 0,6 kg/dm³ |
Wir stellen fest, daß sich das durchschnittliche spezifische Gewicht des Schiffes dem Wert 1
annähert. Würde es ihn erreichen, wäre das Schiff nicht mehr schwimmfähig, sondern könnte nur
noch schweben, ohne daß ein Teil seines Volumens aus dem Wasser herausragt.
Weiterhin haben wir festgestellt, daß das Gewicht eines eingetauchten Körpers (hier also unseres
Schiffes) dem Gewicht der verdrängten Flüssigkeitsmenge entspricht.
Da das Gewicht des Schiffes zugenommen hat, müßte es also auch mehr Wasser verdrängen. Das ist
auch so und das ist leicht von außen erkennbar, denn das Schiff taucht tiefer in das Wasser
ein.
Merke:
| Ein Schiff taucht um so tiefer in das Wasser ein,
je mehr es beladen ist, bzw. je schwerer es ist! |
Dieser Umstand ist für den Schiffsbetrieb von mehrfacher Bedeutung:

| 1.3 Einflußfaktoren auf die Schwimmfähigkeit |
Nach dem bisher Gesagten liegen die Einflußfaktoren auf die Schwimmfähigkeit schon fast auf
der Hand. Es dürfte klar sein, daß hier die ungewollte, bzw. die unerlaubte Gewichtszunahme das
entscheidendende Kriterium ist.
Wieviel Gewichtszunahme jedoch erlaubt ist, bzw. toleriert werden kann, hängt jedoch seinerseits
wieder von verschiedenen Kriterien ab.
1. Die Größe
Je größer das Schiff, desto mehr Ladung kann es tragen. Natürlich, werden Sie sagen, aber man
kann nicht einfach immer größere Schiffe bauen. Der Größe eines Schiffes sind nämlich
unterschiedliche Grenzen gesetzt.
Zum einen wäre da das Fahrtgebiet zu berücksichtigen. Im Binnenbereich ist die maximale Größe
eines Schiffes durch relativ enge Fahrwasser und geringe Wassertiefen beschränkt. Hier bliebe nur
die Möglichkeit, die Schiffe länger zu bauen. Das Bestreben geht tatsächlich in diese Richtung.
Die Verlängerung des Tankmotorschiffes „Joseph Jaegers“ auf 135m und der Bau der
großen Containerschiffe wie z.B. das MS „Yovi“ deuten diese Entwicklung an.
Auch im Seebereich geht die Entwicklung in die gleiche Richtung. Containerschiffe wie die
„Hamburg Express“ und die großen Supertanker haben eine immer größere Ladekapazität.
Aber auch hier stößt man auf ein weiteres Kriterium, welches die Schwimmfähigkeit
beeinflusst:
2. Die Festigkeit
Je mehr die Länge eines Schiffes im Verhältnis zu seiner Höhe und Breite ansteigt, desto mehr neigen die Schiffe dazu, sich durchzubiegen. Außerdem besteht die Möglichkeit, daß sich ein solches Schiff in seiner Länge verdreht. Man sagt dann, daß die Schiffe mit zunehmender Länge biege- und torsionsweich werden. Derartige Biege- und Torsionsbeanspruchungen (z.B. durch Seegang, punktuelle Beladung) belasten die Verbände eines Schiffes und stellen hohe Anforderungen an deren Festigkeit. Der Aufwand, den die Berücksichtigung dieser Umstände erfordert ist sehr hoch und stellt die Wirtschaftlichkeit des Schiffes in Frage, da damit auch die Kosten ansteigen.
Weiterhin hängt die Festigkeit eines Schiffes auch davon ab, aus welchem Material es gebaut wurde. Dem verständlichen Wunsch nach Verringerung des Gewichts durch die Verwendung leichterer Baustoffe (Aluminium, Kunststoffe) kann bestenfalls in Form eines Kompromisses zwischen Gewichtsersparnis und Festigkeit Rechnung getragen werden. Mögliche Störungen durch Eisgang und Grundberührung (z.B. für Fahrzeuge, die in Gebieten mit starkem Tiedenhub verwendet werden) müssen berücksichtigt werden, damit auch in diesen Fällen die Dichtigkeit gewährleistet ist.
3. Die Bauform
Besonders im Seebereich -und hier gilt der Nordatlantik mit seinen Winterstürmen als besonders gefährlich- stellen überkommende Wellen eine Gefahr für das Schiff dar. Bei einem im starken Seegang stampfenden Schiff tauchen die Schiffsenden bisweilen tief in die Wellen ein. Damit sie sich wieder aus den Wellen befreien können, müssen die Schiffsenden genügend Reserveauftrieb zur Verfügung stellen. Daher sind die Schiffsenden zumeist so gebaut, daß sie sich V-förmig nach oben hin verbreitern. Zuviel Auftriebsreserven führen jedoch dazu, daß die Schiffsbewegungen ruckartig erfolgen und damit die Verbände wieder stark belasten. Die beste Form ist also auch hier wieder ein Kompromiß.
4. Die Stabilität
Hier muß genau unterschieden werden zwischen der Festigkeit des Schiffes und seiner
Stabilität. Gemeint ist nämlich nicht seine Fähigkeit, Biege- und Torsionsbeanspruchungen
aufzunehmen (=Festigkeit), sondern die Fähigkeit eines Schiffes, sich aus einer geneigten
(gekrängten) Lage wieder aufzurichten.
Da es sich jedoch um ein sehr komplexes Thema handelt, wurde ihm nachfolgend ein separates
Kapitel gewidmet.

| 1.4 Zusammenfassung |
Ein Körper, der in eine Flüssigkeit getaucht wird, verdrängt genauso viel Flüssigkeitsvolumen,
wie er selbst an Volumen einnimmt.
Ein Körper ist schwimmfähig, wenn sein (durchschnittliches) Spezifisches Gewicht kleiner ist, als
das der Flüssigkeit, in der er sich befindet.
Auf einen Körper, der in Flüssigkeit getaucht wird, wirkt eine Auftriebskraft. Sie ist so groß,
wie die Gewichtskraft der verdrängten Flüssigkeitsmenge.
Für einen vollständig unter Wasser getauchten Körper gilt:
Gewichtskraft > Auftriebskraft der Körper sinkt
Gewichtskraft = Auftriebskraft der Körper schwebt
Gewichtskraft < Auftriebskraft der Körper steigt.
Der steigende Körper durchbricht die Wasseroberfläche. Dadurch verringert sich sein verdrängendes Volumen und damit die Auftriebskraft. Auftriebskraft und Gewichtskraft kommen ins Gleichgewicht und ein Teil des Körpervolumens ragt über die Wasserlinie; er schwimmt.

| 2 Stabilität |
| 2.1 Begriffe |
Im vorangegangenen Kapitel haben wir bereits festgestellt, daß es sich bei der Stabilität
nicht um die Fähigkeit eines Schiffes handelt, Beanspruchungen widerstehen zu können, sondern um
das Vermögen eines Schiffes, sich aus einer geneigten Lage wieder aufrichten zu können.
Wie ausgeprägt diese Fähigkeit ist, hängt in entscheidendem Maße von der Lage des
Gewichtsschwerpunktes und des Formschwerpunktes zueinander ab.
Exkurs:
Gewichtsschwerpunkt ist der Punkt, für den wir uns vorstellen, daß dort die
gesamte
Gewichtskraft des Körpers angreift.
Formschwerpunkt ist der Punkt, für den wir uns vorstellen, daß dort die
gesamte
Auftriebskraft angreift. (siehe auch Kap. 1.1, S. 5)
Eine geneigte Lage kann ein Schiff sowohl über seine Längsachse, als auch über seine Querachse aufnehmen.
Merke:
Die Fähigkeit, sich aus einer Neigung um die Längsachse (Krängung) wieder aufzurichten bezeichnet man als Querstabilität!
Die Fähigkeit, sich aus einer Neigung um die Querachse (Trimm) wieder aufzurichten bezeichnet man als Längsstabilität!
Aufgrund der regelmäßig weit aus größeren Länge des Schiffes im Verhältnis zu seiner Breite, stellt die Längsstabilität von Schiffen i.d.R. Kein Problem dar. Die nachfolgenden Ausführungen beschränken sich daher auf die Querstabilität.

| 2.2 physikalische Grundlagen der Stabilität |
| 2.2.1 Vorüberlegungen |
Um die Vorgänge zu verstehen, die im Zusammenhang mit der Stabilität ablaufen, bedarf es einiger Grundlagen. Eine wesentliche Grundlage sind die Hebelgesetze. Eine in einem bestimmten Punkt angreifende Kraft kann verstärkt werden, wenn wir sie auf einen Hebel einwirken lassen. Es entsteht ein Drehmoment. Physikalisch gesehen ist ein Drehmoment das Produkt aus Kraft und der Länge des Hebelarms, also:
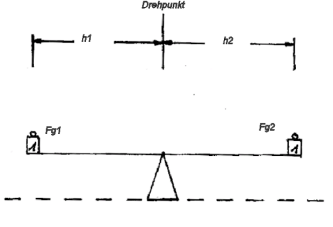
Als einfaches Beispiel für die Wirkung eines Moments kann die Wippe dienen.
 |
 |
In der Skizze greift an beiden Enden eine Kraft an, in diesem Fall die Gewichtskraft. Beide
Gewichtskräfte sind gleich groß und der Punkt, in dem sie angreifen, hat auf beiden Seiten die
gleiche Entfernung zum Lager der Wippe, dem Drehpunkt. Die Wippe befindet sich im Gleichgewicht.
Aus der physikalischen Beschreibung des Drehmoments läßt sich ableiten, daß wir den Wert dieses
Moments verändern können, wenn wir einen der beiden Faktoren verändern, aus denen es sich
zusammensetzt. Das kann entweder die Kraft selbst, oder aber die Länge des Hebels sein, über den
sie wirkt.
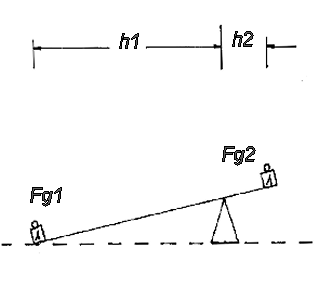
Verschieben wir den Drehpunkt der Wippe, ergibt sich für die eine Seite eine Verlängerung und für
die andere Seite eine Verkürzung des Hebels. Die Gewichte bleiben unverändert, aber trotzdem
befindet sich die Wippe nicht mehr im Gleichgewicht.
 |
 |
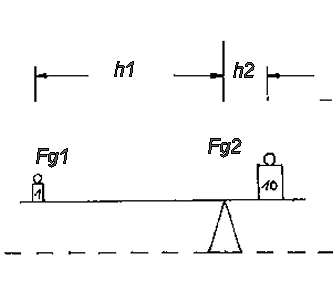
Um sie wieder ins Gleichgewicht zu bringen, müssen wir auf der Seite mit dem kurzen Hebelarm die auf diesen wirkende Kraft vergrößern.
 |
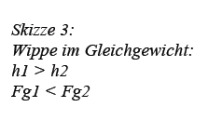 |
Außerdem dürfte klar sein, daß wenn einer der beiden Faktoren eines Moments den Wert
„0“ hat, auch das gesamte Moment „0“ ist.
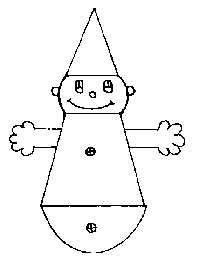
Vielleicht ist dem Einen oder Anderen noch aus Kindheitstagen das „Stehaufmännchen“
bekannt.
Auf einer Halbkugel aus Blei oder einem anderen schweren Material ist eine Figur aus einem sehr
leichten Material gesetzt und egal, in welchem Maß wir die Figur in eine Schieflage bringen, sie
kehrt immer wieder in ihre aufrechte Position zurück.
 |
 |
Das liegt daran, daß der Schwerpunkt der Figur durch den schweren Fuß sehr weit nach unten
gerückt ist. Er befindet sich in Ruhelage genau über der Auflagefläche. Drehen wir das Männchen
zur Seite, so liegt die Halbkugel mit einem anderen Punkt auf. Die Lage des Schwerpunktes bleibt
unverändert, jedoch liegt er nun nicht mehr genau über der Auflagefläche, sondern erhält zu
diesem einen seitlichen Abstand.
Dieser seitliche Abstand fungiert als Hebel, über den die Gewichtskraft des Fußes nun wirkt. Es
entsteht ein Drehmoment, das das Männchen wieder aufrichtet.
Weiterhin ist von Bedeutung, in welche Richtung das Drehmoment wirkt, insbesondere dann, wenn
mehrere Momente gleichzeitig auf einen Körper einwirken.
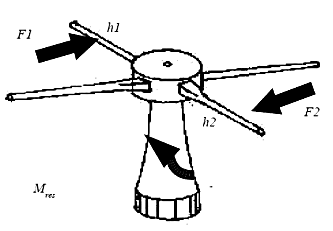
Wirken beide Momente so, daß sie beide eine Drehung in die selbe Richtung ergeben, so addieren
sie sich. Die Hebel beider Momente und die Kräfte kann man sich dann als einen einzigen Hebel und
eine einzige Kraft vorstellen, deren Werte sich aus den entsprechenden Summen ergeben.
 |
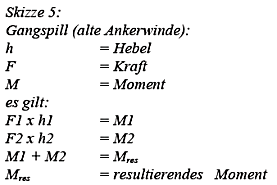 |
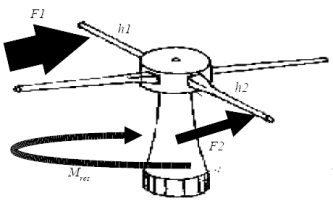
Wirken beide Momente in entgegengesetzter Richtung, entscheidet das größere Moment, in welche Richtung das System letztlich dreht.
 |
 |
Das größere Moment reduziert sich um den Wert des kleineren und ergibt ein resultierendes Moment.
| 2.2.2 Gewichtsstabilität |
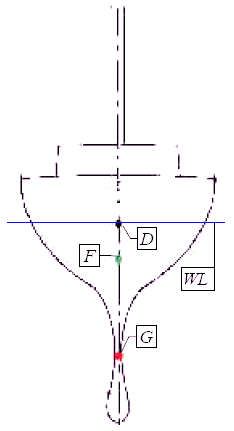
Ähnlich verhält es sich mit Schiffen, die an einem tief reichenden Schwert einen Bleiballast fahren.
 |
 |
Wenn Sie die Skizzen des Stehaufmännchens und der Kielyacht miteinander vergleichen, fällt Ihnen vielleicht eine Gemeinsamkeit auf: In beiden Fällen liegt der Gewichtsschwerpunkt unterhalb des Formschwerpunktes.
Merke:
| Liegt der Gewichtsschwerpunkt unter dem Formschwerpunkt,
dann ist das Schiff gewichtsstabil! |
Darüber hinaus ist beiden gemeinsam, daß es einer Kraft bedarf, sie überhaupt erst in die
geneigte Lage zu bringen. Beim Stehaufmännchen ist das der Finger, bei dem Schiff könnte das z.B.
der Wind sein. Dann vollführen beide eine Drehung um ihren Drehpunkt.
Der Kraftaufwand, der dazu nötig ist, ist um so geringer, je höher der Punkt liegt, an dem diese
Kraft angreift, weil auch hier wieder die Entfernung vom Angriffspunkt der neigenden Kraft zum
Drehpunkt als Hebel fungiert.
Die Lage des Drehpunktes um den ein Schiff sich bei einer
Krängung dreht ist nur schwer bestimmbar, da sie von vielen
Faktoren abhängig ist, u.a. von der Symmetrie des
eingetauchten Teils des Schiffes und der Lage des
Formschwerpunktes. Für unsere weiteren Überlegungen
nehmen wir der Einfachheit halber an, daß er im Bereich des
Schnittpunktes der Wasserlinie mit der vertikalen
Mitschiffsebene liegt.
Der Genauigkeit zuliebe sprechen wir also nachfolgend nicht von einer krängenden Kraft,
sondern von einem krängenden Moment! Entfällt nun das Moment, das die Yacht geneigt hat, so
erwarten wir nichts Anderes, als daß sie sich wieder aufrichtet. Dies kann sie aber nur, wenn sie
wiederum eine Drehung um den Drehpunkt vollführt, dieses Mal jedoch in die genau entgegengesetzte
Richtung.
Um diese Drehung stattfinden zu lassen bedarf es ebenfalls eines Momentes, welches wir jedoch, da
es dazu führt, daß der Körper wieder in seine aufrechte Lage zurückkehrt das aufrichtende Moment
nennen. Auch für dieses Moment gilt:
d.h. wir benötigen wieder eine Kraft, die über einen Hebelarm wirkt. Würde es dieses
aufrichtende Moment nicht geben, würde der Körper in der von ihm zuletzt eingenommenen Lage
verharren. Was bleibt, um zu verstehen, warum sich der Körper doch wieder aufrichtet, ist zu
untersuchen, woher die für das aufrichtende Moment notwendigen Kräfte und Hebel stammen, bzw. wie
sie entstehen.
Da wir in unseren Überlegungen davon ausgehen, daß die für das krängende Moment nötige Kraft, und
mit ihr das gesamt krängende Moment entfallen ist, verbleiben für das aufrichtende Moment nur
noch zwei Kräfte, die die ganze Zeit über auf unser Schiff eingewirkt haben und immer noch
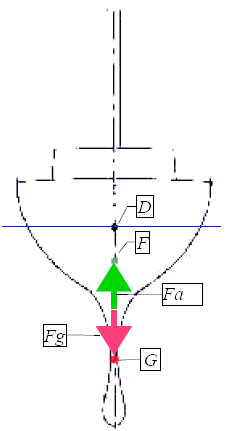
wirken: die Gewichtskraft und die Auftriebskraft. Tatsächlich sind beide an der Entstehung des
aufrichtenden Moments beteiligt.
 |
 |
In einer gekrängten Lage verändert sich auch die Position der beiden Schwerpunkte zueinander.
Das wäre schon der Fall, wenn beide Schwerpunkte innerhalb des Schiffes ihre Position beibehalten
würden. Zumindest der Formschwerpunkt tut dies aber nicht (siehe hierzu Ausführungen Kap. 1.1, S.
5). Er wandert zunächst einmal in der Richtung aus, in der der tiefer eingetauchte Teil des
Schiffes liegt.
Durch die Krängung einerseits und das Auswandern des Formschwerpunktes andererseits erhalten die
beiden Schwerpunkte, die bei aufrechter Lage des Schiffes genau übereinander gelegen haben nun
einen seitlichen Abstand zum Drehpunkt und zueinander und mit ihnen die Wirklinien der in diesen
Punkten angreifenden Kräfte.
Der seitliche Abstand, den der Gewichtsschwerpunkt zum Drehpunkt hat, ist die Länge des Hebels,
über den die Gewichtskraft wirkt.
 |
 |
Das gleiche gilt für die Auftriebskraft.
Es entstehen zwei Momente, die beide eine Drehung in die gleiche Richtung bewirken. Weil sie
beide in die gleiche Richtung wirken, können wir vereinfacht sagen:
Merke:
| Der seitliche Abstand zwischen den Schwerpunkten und damit zwischen den Wirklinien der in diesen Punkten angreifenden Kräfte stellt die Länge des Hebels für das aufrichtende Moment dar. |
Richtet sich das Schiff unter Einwirkung des Moments wieder auf, verändert sich die Lage der Schwerpunkte zueinander wieder, ihr seitlicher Abstand und damit die Länge des Hebels des aufrichtenden Moments wird kleiner, bis die Punkte wieder übereinander liegen. Der seitliche Abstand, d.h. der Hebel beträgt „0“ und damit das gesamte Moment. Das Schiff schwimmt wieder aufrecht.
| 2.2.3 Formstabilität |
Es ist ein Trugschluß anzunehmen, daß ein Schiff, dessen Formschwerpunkt unterhalb des Gewichtsschwerpunktes liegt nicht mehr in der Lage ist, sich aus einer gekrängten Lage wieder aufzurichten.
Merke:
| Liegt der Gewichtsschwerpunkt über dem Formschwerpunkt, dann ist das Schiff formstabil! |
Auch Binnenschiffe sind fast ausnahmslos formstabil. Bedingt durch ihr Fahrtgebiet, in denen
niedrige Wasserstände eher die Regel sind, als die Ausnahme, können sie schon gar nicht so gebaut
sein, daß man unter ihren Rumpf einen Ballast anbringen könnte, der ihren Gewichtsschwerpunkt
unter den Formschwerpunkt bringt. Ein Spaziergang am Rheinufer jedoch führt uns direkt vor Augen,
daß trotzdem Binnenschiffe in der Lage sind, eine aufrechte Position zu halten, bzw. wieder
einzunehmen.
Das bedeutet, daß auch bei formstabilen Schiffen ein Moment existieren muß, das es aus einer
gekrängten Lage heraus wieder in die aufrechte bringt.
Dem ist tatsächlich so und wie bei der Gewichtsstabilität sind es wieder die Auftriebskraft und
die Gewichtskraft, die an der Entstehung des aufrichtenden Moments beteiligt sind. Doch schauen
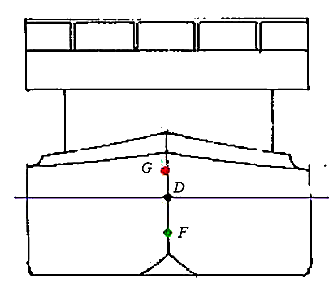
wir uns zunächst einmal ein formstabiles Schiff und die Lage seiner Schwerpunkte etwas genauer
an.
 |
 |
Nimmt nun das Schiff durch äußere Einflüsse eine gekrängte Lage ein (z.B. durch Winddruck,
oder aber auch durch die auf das Schiff wirkende Zentrifugalkraft bei einer Kurvenfahrt), findet
statt, was wir schon bei der Gewichtsstabilität festgestellt haben: Die Schwerpunkte verändern
ihre Position zueinander.
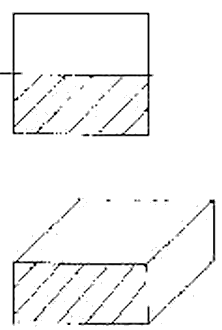
Weil sich die Form des eingetauchten Teils des Schiffs (und nur des eingetauchten Teils, nicht
etwa die des Schiffes an sich) verändert, verlagert sich darüber hinaus der Formschwerpunkt
relativ zu seiner eigenen, ursprünglichen Lage.
 |
 |
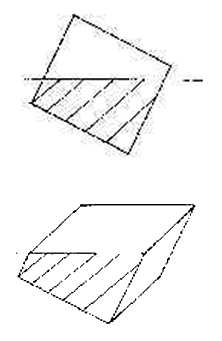 |
Er wandert aus, in Richtung der tiefer eingetauchten Seite. Das Volumen, mit dem das Schiff eintaucht bleibt aber gleich!
Natürlich greifen auch hier die Gewichtskraft im Gewichtsschwerpunkt und die Auftriebskraft im Formschwerpunkt, d.h. im neuen, ausgewanderten Formschwerpunkt an.
 |
 |
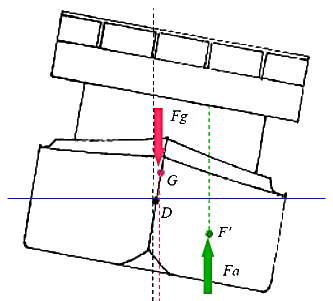
Anhand der Skizze können wir schon sehen, daß auch in diesem Fall die Wirklinien der Kräfte
einen seitlichen Abstand zum Drehpunkt erhalten haben. Auch hier fungiert dieser seitliche
Abstand zwischen den Wirklinien und dem Drehpunkt als Hebelarm, der mit den über ihn wirkenden
Kräften je ein Moment bildet. Die Gewichtskraft bildet über ihren Hebel ein Moment, welches das
Schiff weiter krängen lassen will. Die Auftriebskraft bildet mit ihrem Hebel ein Moment, welches
das Schiff wieder aufrichten will. Welches Moment gerade das größere ist, ist davon abhängig,
welches Moment den längeren Hebelarm besitzt, da die wirkenden Kräfte ja gleich groß sind
(archimedisches Prinzip).
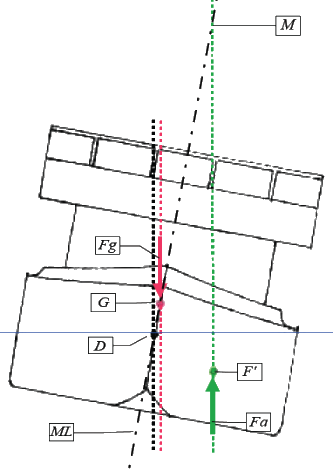
Um das zu überprüfen, reicht die obige Skizze nicht ganz aus. Wir müssen sie etwas erweitern.
Zeichnen wir in den Schiffskörper eine Achse ein, die ihn in vertikaler Richtung halbiert und
verlängern die Wirklinie der Auftriebskraft nach oben, so ergibt sich irgendwann ein Schnittpunkt
dieser beiden Linien.
Dieser Schnittpunkt wird Metazentrum (M) genannt und seine Lage ist von entscheidender Bedeutung
für die Beurteilung, ob es sich bei dem resultierenden Moment um ein aufrichtendes oder ein
krängendes handelt.
Merke:
| Solange das Metazentrum über dem Gewichtsschwerpunkt liegt, handelt es sich bei dem entstandenen Moment um ein aufrichtendes! Liegt das Metazentrum unterhalb des Gewichtsschwerpunktes, handelt es sich um ein krängendes Moment! |
Sollte das Metazentrum unterhalb des Gewichtsschwerpunktes liegen hat das schlimme Folgen für das betroffene Schiff: es kentert! Dann nämlich ist der Hebelarm, an dem die Auftriebskraft angreift kürzer, als der Hebelarm, über den die Gewichtskraft wirkt.
 |
 |
In dieser Skizze liegt das Metazentrum über dem Gewichtsschwerpunkt. Nach Wegfall der
Einflüsse, die es in die gekrängte Lage gebracht haben, wird es sich wieder aufrichten, da die
Auftriebskraft über den längeren Hebel verfügt. Richtet sich das Schiff unter Einfluß der über
den längeren Hebel wirkenden Auftriebskraft auf, verkleinern sich die Hebel beider Momente und
zwar so lange, bis die beiden Schwerpunkte wieder genau übereinander liegen. Sie liegen dann auf
einer Ebene mit dem Drehpunkt, die Folge: kein seitlicher Abstand der Kräftewirklinien zum
Drehpunkt mehr, d.h. kein Hebel mehr und daher auch keine Momente. Das Schiff schwimmt aufrecht.
Es ist aber denkbar, daß der krängende Einfluß nicht entfällt, sondern im Gegenteil sogar
zunimmt. Die Krängung verstärkt sich und das u.U. sogar so weit, daß auf der Leeseite
(windabgewandten Seite) des Schiffes die Deckskante unter die Wasserlinie gerät.
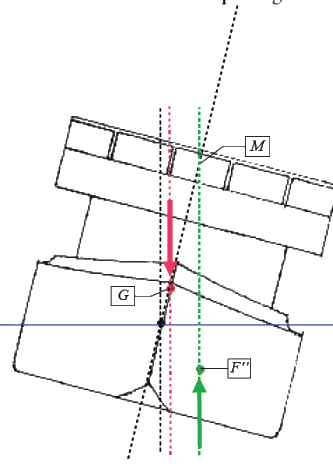
Wenn das geschieht, besteht höchste Gefahr für das Schiff! Die Form des Unterwasserschiffes
ändert sich nun noch drastischer, als bis zu diesem Zeitpunkt. Diese Formänderung kann bewirken,
daß sich der Formschwerpunkt so verlagert, daß sich der seitliche Abstand zwischen den beiden
Schwerpunkten verringert. Das bedeutet auch eine Verkürzung des Hebels des aufrichtenden Moments
und damit eine Verringerung des resultierenden aufrichtenden Momentes an sich!
Eine Verlängerung der Wirklinie der Auftriebskraft nach oben ergibt ein Metazentrum, das sich auf
der vertikalen Mittschiffsachse nach unten verlagert hat, d.h. sich dem Gewichtsschwerpunkt
genähert hat.
 |
 |
Es ergibt sich ein Beziehungsgeflecht zwischen dem Abstand des Metazentrums zu dem Gewichtsschwerpunkt und der Länge des Hebels des aufrichtenden Moments.
Merke:
| Der Abstand zwischen Metazentrum und Gewichtsschwerpunkt wird metazentrische Höhe genannt und ist ein wichtiges Maß für die Stabilität formstabiler Schiffe! |
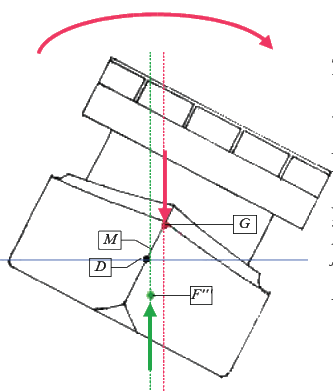
Angenommen, die Krängung des Schiffes nimmt noch weiter zu. Irgendwann hat sich der
Formschwerpunkt so weit verlagert, daß die nach oben verlängerte Wirklinie der in ihm
angreifenden Auftriebskraft die Mittschiffsachse unterhalb des Gewichtsschwerpunktes schneidet
und somit das Metazentrum unter ihm liegt.
Es existiert immer noch ein seitlicher Abstand zwischen den Wirklinien der Auftriebskraft und der
Gewichtskraft, also auch immer noch ein Moment.
Die Wirkung dieses Moments hat sich jedoch ins Gegenteil verkehrt. Es ist zu einem krängenden
Moment geworden, weil es nun die Gewichtskraft ist, die über den längeren Hebel verfügt und das
Schiff wird unweigerlich kentern!
 |
 |
Kontrollfragen:
1. Welche Art der Stabilität kommt sinnvoller Weise nur für ein U-Boot in Betracht?
2. Wie wirkt sich zusätzliche Beladung eines Schiffes auf dessen Stabilitätszustand aus?

| 2.3 Zusammenfassung |
Ein Schiff, dessen Gewichtsschwerpunkt unter dem Formschwerpunkt liegt ist gewichtsstabil.
Ein Schiff, dessen Gewichtsschwerpunkt über dem Formschwerpunkt liegt ist formstabil
Wird das Schiff gekrängt, verändert sich die Form des eingetauchten Teils des Schiffes. Mit der Formänderung ändert sich auch die Lage des Formschwerpunktes. Er wandert zu der tiefer eingtauchten Seite aus.
Sowohl Form-, als auch Gewichtsschwerpunkt erhalten einen seitlichen Abstand zu der Ebene, auf der der Drehpunkt des Schiffes für eine Drehung um die Längsachse (= Krängung) liegt.
Der seitliche Abstand der Wirklinien der Kräfte zur Ebene des Drehpunktes fungiert als Hebel, über den die Kräfte wirken und somit ein Moment bilden.
Der Abstand der Kräftewirklinien untereinander entspricht der Länge des Hebels für das aus beiden resultierende Moment.
Die Wirklinie der Auftriebskraft schneidet die vertikale Mittschiffsachse im Metazentrum.
Liegt das Metazentrum über dem Gewichtsschwerpunkt, fungiert das resultierende Moment als aufrichtendes Moment, liegt das Metazentrum unter dem Gewichtsschwerpunkt, fungiert das resultierende Moment als krängendes Moment.
Ist das resultierende Moment ein krängendes, kentert das Schiff.
Der Abstand zwischen Metazentrum und Gewichtsschwerpunkt wird als metazentrische Höhe bezeichnet.
Ausgewählt von Peter Schuster ergänzend ein paar Szenen zum Thema Stabilität, Kentern, aufrichtendes Moment, usw...
 |
 |
 |
 |
 |
 |
 |



