Baupraxis
|
|
Modellbau
Baupraxis |
mini-sail e.V. |
Peter Schuster und ich sind bei Unterhaltungen über den von mir verfaßten und bereits auf unserer Homepage veröffentlichen Artikel darauf gestoßen, wie breit gefächert selbst ein so spezielles Thema wie der Decksbalken, als nur ein Bauteil im Gebäude "Schiff" sein kann.
Um einmal darzustellen, wie breit dieses, und auch alle anderen Themen im Schiffbau ausgewalzt werden kann und auch um zu zeigen, daß die Angaben in der so genannten Fachliteratur nicht immer der Weisheit letzter Schluß sind, habe ich diesen Artikel noch einmal überarbeitet und wesentlich ergänzt.
Hier das Ergebnis:
Die Decksbalken der Schiffe sind nach oben gekrümmt. Diese Krümmung nennt man Bucht. Als Höhe der Bucht verstehe ich, um wie viel die Balkenmitte in der Horizontalen höher liegt, als dessen Ende (oder Anfang, wie man will).
Duhamel du Monceau schreibt in "Anfangsgründe der Schiffsbaukunst" 1798:
Die Verdecks-Balken mussen einige Aufbugt haben, theils damit das Wasser von den Verdecken ablaufe, theils auch in der Absicht, um den Rücklauf des Geschützes zu vermindern, und dasselbe leichter wieder gegen Bord an bringen zu können.
Nun gut, daß die Balken "einige Aufbugt" haben müssen, darüber sind sich wohl (fast) alle einig. Da hört die Einigkeit dann aber auch schon auf, denn
Klawitter schreibt 1835 in "Vorlegeblätter für Schiffbauer":
Bei Kriegsschiffen ist diese Aufbugt gewöhnlich kleiner, weil sie den Bewegungen und besonders dem Rücklauf der Geschütze hinderlich ist
Na so was, der eine sieht also in einer starken Balkenbucht einen Vorteil für die Geschützbedienung, der Andere empfindet den gleichen Umstand als Nachteil. In die moderne Fachliteratur hat dieser Gegensatz natürlich keinen Eingang gefunden, er wird totgeschwiegen, würde er doch alles zu sehr verkomplizierten. Anstelle dessen wird in Kauf genommen, daß sich Modellbauer mit ihren unterschiedlichen, aber jeweils natürlich authentisch belegbaren Auffassungen in die Wolle bekommen. Mondfeld, Curti und Co. behandeln das Thema wohl bewußt sehr oberflächlich.
Mondfeld bietet für die Konstruktion der Krümmung eine Schablone an, verschweigt aber, wie er selbst diese konstruiert hat und daß diese Schablone nur eine Möglichkeit von unendlich vielen ist.
Aber lassen wir Monceau, Steinhaus und Konsorten weiter zu Wort kommen. Klawitter schreibt:
Die Verdecksbalken tragen zur Festigkeit des Schiffes viel bei und dienen hauptsächlich zur Zusammenhaltung desselben, damit es in der Breite nicht ausweichen kann. Man giebt diesen Balken eine Krümmung oder Bugt nach oben, damit das Regen- oder Seewasser, welches häufig auf das Verdeck fällt, sich an den Seiten sammeln, und durch die sogenannten Speigaten (Abgußröhren) nach außen zu abgeführt werden kann.
Diese Aufbugt beträgt bei Kauffahrteischiffen den 4ten Theil der Länge des Balkens nach Fußen in Zollen ausgedrückt. Wäre demnach der Balken 24 Fuß lang, so würde seine Aufbucht 24/4= 6 Zoll betragen. (Schreibweise wurde so aus dem Original übernommen).
In "Die Schiffbaukunst in ihrem ganzen Umfange" schreibt Steinhaus 1858:
Bei der Aufschnürung für die Bucht der Decksbalken ist besonders darauf zu achten, daß sie überall eine gleichmäßige Krümmung erhält und so einen Kreisabschnitt bildet.
Hier haben wir den Grund dafür gefunden, weshalb ich nach einem Weg gesucht habe, den Radius des Kreises zu bestimmen, dessen Abschnitt die Krümmung des Decksbalkens darstellt.
Klawitter bietet auch eine grafische Methode zur Konstruktion der "Bugt", wie er schreibt, an (Blatt IV seiner "Vorlegeblätter..."), ohne den Radius zu kennen (am Ende dieses Artikels stelle ich diese Methode auch noch kurz vor). Nachteil ist, daß über diese Methode nur eine Anzahl von Punkten definiert wird, die zu einer Kurve verbunden werden müssen. Die Genauigkeit dieser Methode steigt mit der Anzahl der definierten Punkte, bleibt aber immer hinter der eines mit dem Zirkel gezeichneten Kreisabschnittes zurück und macht nur bei Platzproblemen Sinn (bei meiner Yacht im Maßstab 1:15 zum Beispiel wäre der Decksbalken im Original 5,70m lang, der Kreisradius für die Balkenbucht betrüge über 26 m (!!) und ein Zirkel mit diesem Radius wäre kaum noch zu handhaben).
Bei unseren Modellen braucht man kaum mit Decksbalken von mehr als 50 cm Länge zu rechnen und da bleibt der zugehörige Radius recht gut zu handhaben (Bleistift an Bindfaden).
Die Methode ist eigentlich etwas für Leute, die den Anspruch erheben, alles ganz genau und genau nach histerischem..., Verzeihung, historischem Vorbild machen zu wollen. Ich wundere mich, beim Arbeitskreis, oder bei der Minisail Classic noch nichts darüber gelesen zu haben.
Auf der Homepage der Swiss-Mini-Sail wird die Problematik mit der schlichten Formel: r= 4,5B abgehandelt, wobei r der Radius des Kreises ist und B die Länge des untersuchten Decksbalkens. Diese Methode reicht wohl für die meisten Modellbauer völlig aus, ist aber natürlich noch nicht einmal die Hälfte der ganzen Wahrheit. Sie läßt für jede Decksbalkenlänge nur eine einzige Höhe der Bucht zu. Wie wir aber aus den o.a. Zitaten entnehmen können, gab es da durchaus Unterschiede. Einige Schiffe fuhren stark gekrümmte Balken, einige hatten fast ebene Decks. Teilweise waren die Krümmungen der Decks auf ein und demselben Schiff unterschiedlich. Diese Unterschiede können mit meinem Weg berücksichtigt werden.
Übrigens ist es ein Irrglaube anzunehmen, man brauche nur den längsten Decksbalken eines Decks zu konstruieren und könne diesen dann als Schablone für alle anderen Balken des selben Decks verwenden. So kann man z.B. bei genauer Betrachtung der Pläne in der Architectura Navalis Mercatoria feststellen, daß die Aufbuchtung der Decksbalken zum Bug hin kleiner wird. Das macht auch Sinn, denn die Decksplanken liegen im Bugbereich auf Innenhölzer, den Bugbändern auf und deren Verlauf weist in der Horizontalen keine Bucht auf. Somit müßte man eigentlich für jeden Decksbalken die Aufbucht an seinem Liegeplatz separat ausmessen und in die Berechnung der Krümmung mit einfließen lassen.
Ich selbst sehe diese Methode eher als Spielerei an (Auweia, Spielerei dürfte ich ja gar nicht sagen, Modellbauer betreiben ihr Hobby ja ernsthaft ;-) ), weil ein Deck, das nach dieser Methode entworfen wurde wahrscheinlich bei bloßem Hinschauen genau so gut daher kommt, wie ein mit dem Kurvenlineal gezeichnetes. Insofern betrachte es als ein Angebot, dessen Bedeutung ich nicht allzu hoch einschätzen würde.
Versteht man also die Krümmung des Decksbalkens als einen Abschnitt eines Kreisumfanges, so gilt es für die Konstruktion eines einwandfrei gekrümmten Decksbalkens den Radius des dazu gehörenden Kreises zu bestimmen. Dies ist mit ein bißchen Geometrie und den Winkelfunktionen ohne Weiteres möglich. Ich beziehe mich mit der Bezeichnung der Seiten auf die Skizze.
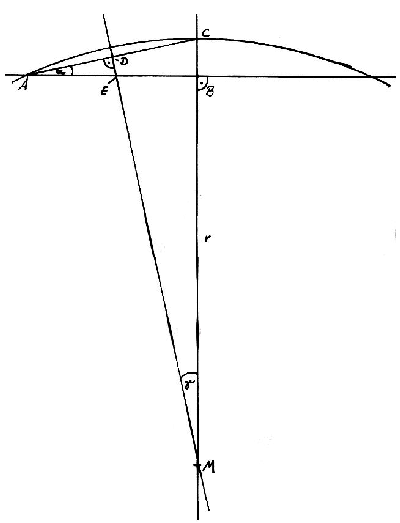
Gesucht:
Strecke MC (= r).
Bekannt: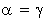
Vorgehensweise:
Die beiden Dreiecke ABC und CDM sind sich geometrisch ähnlich, somit auch der Winkel CAB (= 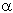 ) und der Winkel DMC (=
) und der Winkel DMC (= 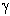 )
)
Von dem Dreieck ABC sind die meisten Größen bekannt. Es fehlt nur noch die Länge der Strecke AC, die sich leicht über den Satz des Pythagoras ermitteln läßt.
Kathede² + Kathede² = Hypotenuse² =>
AB² + BC² = AC² =>
AC = 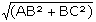
Ist AC bekannt, ist auch CD bekannt, da CD ja AC : 2 ist (siehe zu bekannt 5.).
Mit der bekannten Strecke BC (= Gegenkathede zu 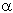 ) und der nunmehr bekannten Strecke AC (= Hypotenuse) läßt sich der Sinus von a und damit der Winkel selbst errechnen.
) und der nunmehr bekannten Strecke AC (= Hypotenuse) läßt sich der Sinus von a und damit der Winkel selbst errechnen.
Da gilt, daß 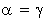 , ist nun auch
, ist nun auch 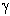 bekannt.
bekannt.
Der Sinus von 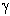 ist CD (Gegenkathede) : MC (= r = Hypotenuse) und natürlich identisch mit dem Sinus von
ist CD (Gegenkathede) : MC (= r = Hypotenuse) und natürlich identisch mit dem Sinus von 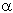 und somit ebenfalls bekannt. Durch Umstellen der Gleichung:
und somit ebenfalls bekannt. Durch Umstellen der Gleichung:
sin 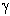 = CD : MC erhält man MC = CD : sin
= CD : MC erhält man MC = CD : sin 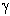
MC ist der Radius (r) des Kreises, dessen Teilabschnitt des Umfanges die Krümmung des Decksbalkens darstellt.
Durch Umstellen, Einsetzen usw. kann man dann eine für alle Decksbalken gültige Formel entwickeln, wobei es vollkommen gleichgültig ist, in welchem Verhältnis die Länge des Balkens zu seiner Bucht steht. Sie lautet:
r= (AB²+BC²) : 2 BCwobei r der gesuchte Radius ist, AB die halbe Decksbalkenlänge und BC die Höhe der Bucht. Bei der Verwendung der Formel sind natürlich die mathematischen Grundregeln zu beachten, insbesondere Punkrechnung vor Strichrechnung, Potenzrechnung vor Punktrechnung Wer noch wissen will, wie ich diese Formel entwickelt habe, der kann jetzt noch ein bißchen weiter lesen. Wen Formeln eher verwirren, sollte hier aufhören, obwohl es sich eigentlich nur um Algebra der 8. und 9. Klasse handelt.
Da CD= AC : 2 ist und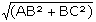 ist, gilt
ist, gilt
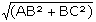 ) : 2
) : 2
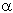 , gilt
, gilt
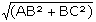 ) : 2 ) : sin
) : 2 ) : sin 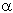
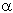 = Gegenkatede : Hypothenuse, also BC : AC ist, gilt
= Gegenkatede : Hypothenuse, also BC : AC ist, gilt
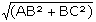 ) : 2 ) x AC : BC
) : 2 ) x AC : BC
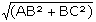 =>
=>
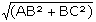 ) : 2 ) x
) : 2 ) x 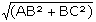 : BC =>
: BC =>
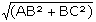 )² : 2 BC =>
)² : 2 BC =>
Der Vollständigkeit halber sei hier noch kurz die Methode beschrieben, die Klawitter in seinen Vorlegeblättern vorschlägt.
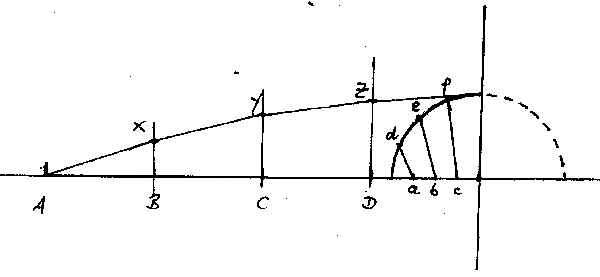
Die Länge des Decksbalkens wird als Gerade gezeichnet und seine Mitte markiert.
Diese Balkenmitte ist auch Mittelpunkt eines zu zeichnenden Kreises, dessen Radius der vorgesehenen Höhe der Bucht entspricht. Von diesem Kreis betrachten wir zunächst nur eines der Viertel, die auf der anfangs gezeichneten Geraden liegen.
Der Umfang dieses Viertelkreises wird in, sagen wir vier gleich lange Abschnitte geteilt, wodurch sich die Punkte d, e und f ergeben.
In eben so viele Abschnitte unterteilen wir den Radius des Kreises auf der anfangs gezeichneten Geraden und erhalten so die Punkte a, b, und c und die zu untersuchende Decksbalkenhälfte, so daß sich hier die Punkte A, B, C, D ergeben.
Wir verbinden nun die Punkte a und d, b und e und c und f miteinander und erhalten so Geraden mit einer bestimmten Länge.
Die Strecke ad wird senkrecht über Punkt B, die Strecke be senkrecht über Punkt C und die Strecke cf senkrecht über Punkt D angetragen.
Es ergeben sich die Punkt X, Y und Z, die Punkte auf der Decksbalkenoberfläche sind und noch zu der gesuchten Krümmung miteinander verbunden werden müssen.



